Once the basic characteristics of the control strategy is formulated in the reduced-dimensional space, where intuition is strong, one needs to "map" the strategy back to the full dynamic model of the humanoid for an implementation ready control law.

While useful in their own right, a limitation of the above models is that they represent the entire humanoid body only as a point mass and do not characterize the significant centroidal moment of inertia of the humanoid body. The centroidal moment of inertia is a property of the distributed masses of the robot limbs (head, arms, legs, etc) away from the CoM. We have demonstrated that a humanoid's state of balance is closely related to its rotational equilibrium which, in turn, is dependent on its angular momentum rate change. The centroidal moment of inertia directly contributes to the centroidal angular momentum and its rate of change. Direct manipulation of momenta is becoming a reasonable, and sometimes preferable, way to control a robot.

We present the Reaction Mass Pendulum (RMP) model as an extension of the traditional inverted pendulum models. The RMP model explicitly models the robot's extended intertia by means of its instantaneous centroidal composite rigid body inertia (CCRBI) matrix. CCRBI matrix is identical to the so-called locked inertia and represents the aggregate rigid body inertia of entire humanoid computed at its CoM, assuming that its joints are temporarily locked. It is a single rigid-body approximation of the multi-body humanoid.

An RMP consists of two components, a ``leg'' that joins the CoP and the CoM, and an ellipsoidal ``body'' -- the abstracted reaction mass -- that characterizes the generalized inertia of the entire robot projected at the CoM. As the robot moves in space, so does the RMP, resulting in a continuous movement of the CoP and CoM. All limb movements of the robot affect its centroidal moment of inertia, which is captured by the changing shape, size and orientation of the ellipsoidal reaction mass.

The reaction wheel or inertia wheel is one of a number of standard momentum exchange devices that are used to control satellite orientation. An actuated reaction wheel attached to a rigid rod becomes a reaction wheel pendulum.

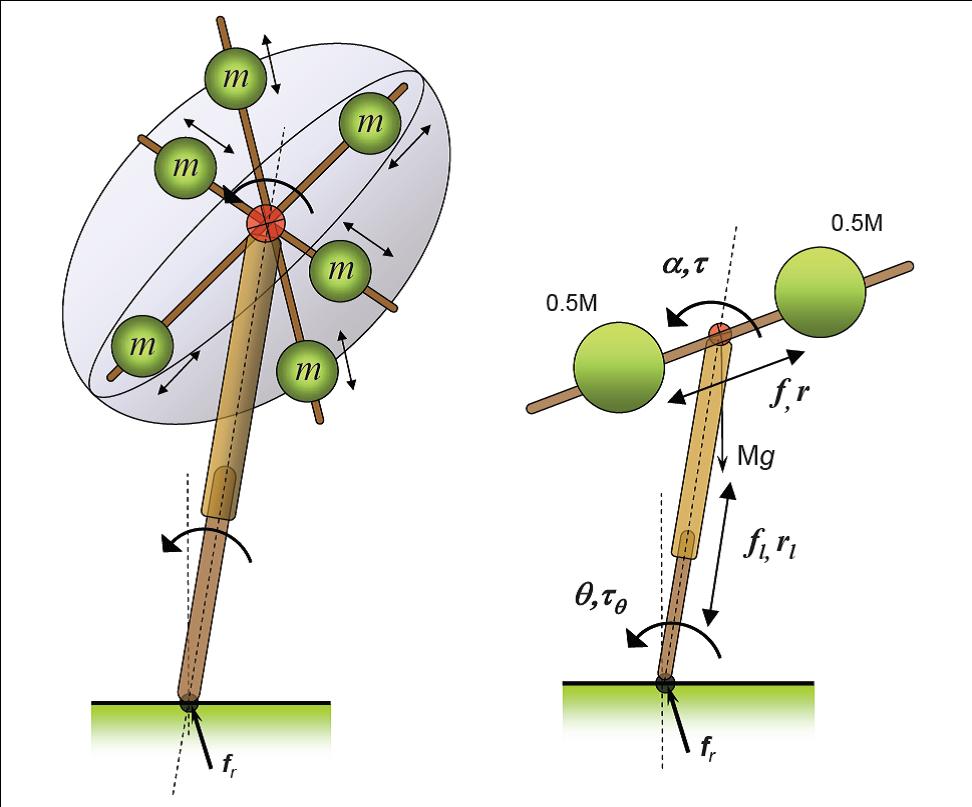
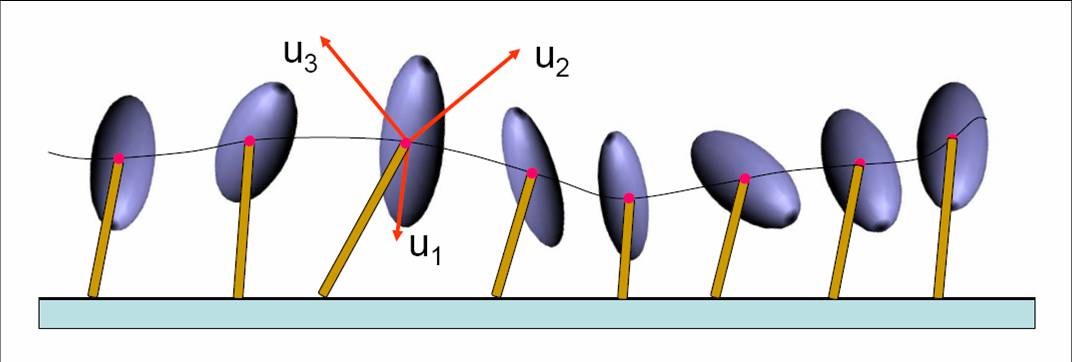
The 3D reaction mass has continuously variable inertia. At any given configuration of the robot, the centroidal rigid body inertia can be reduced to an ellipsoid.

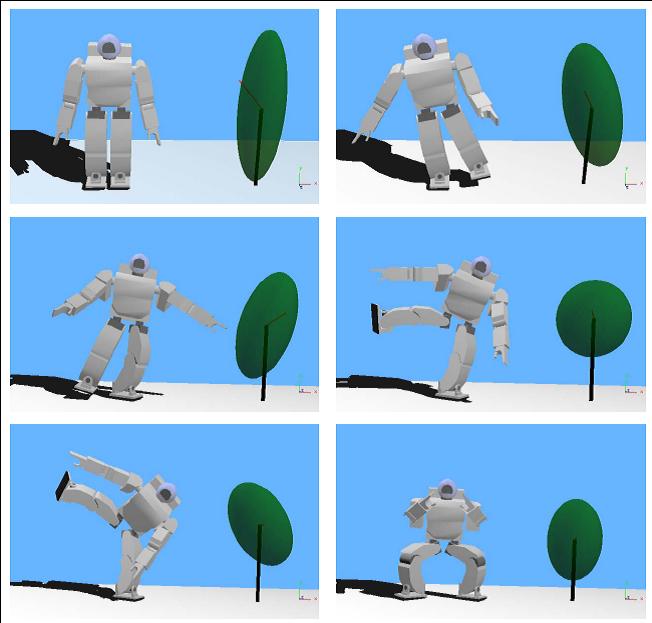
Inertia Shaping

An interesting application of the RMP modeling approach is what we call inertia shaping of an articulated chain. Inertia shaping is a high-level approach to precisely control the aggregate kinodynamic characteristics of an articulated chain by controlling its CRB inertia. Given a desired CRB inertia from the RMP model, the humanoid should make a proper pose to achieve this goal. This can be posed as an inverse kinematics problem with the desired CRB inertia constraints. Since we have derived the CRB inertia Jacobian, the inverse kinematics problem can be solved by any suitable optimization algorithm. The simplest solution will be updating desired joint angles using the pseudo-inverse of CRB inertia Jacobian.

The following figure presents three examples of inertia shaping on a non-contacting biped floating in space (say, a humanoid astronaut). The robot is given three different commands, shown in series a, b, and c, respectively, to try to match its own CRB inertia to a desired CRB inertia. Starting from an initial configuration, the robot moves its joints such that the cost function, the Frobenius norm of the difference between the two inertias, is minimized.

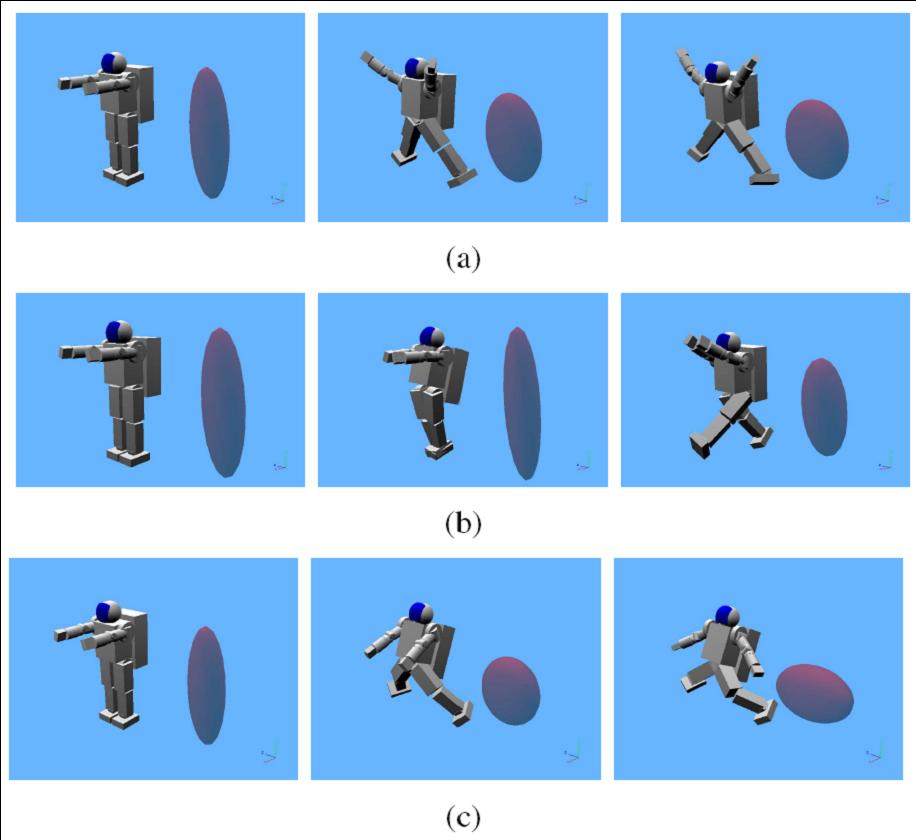
In Fig. a, the desired inertia components along all three axes are equal and large. Hence the robot tries to "expand" in all directions. In Fig. b, the desired inertia along Y-axis (vertical) is big, and the other directions are very small. In Fig. c, robot tries to make its inertia along X and Z larger at the cost of Y-direction.

This simulation demonstrates the important point of effectively controlling a complex biped with a very simple control law. While the robot model has 27 dofs, the control law deals with only three variables which are the three diagonal elements of the robot's rotational inertia.