Centroidal Moment Pivot (CMP) Point:
|
|
A humanoid robot is said to possess linear stability if the external
forces sum up to a zero resultant force. Similarly, the robot is
considered rotationally stable if the resultant external forces
and moments, computed at its overall CoM (or, centroid), sum up to a zero moment.
According to a fundamental principle of mechanics, the resultant
external moment on a humanoid robot is equal to the rate of
change of its angular momentum. In other words, for a rotationally
stable humanoid robot, one that is not tipping over, the
centroidal angular momentum rate change is zero. The
angular momentum of the system is conserved.
For a legged robot external force/moments may arise from gravity, ground contacts, additional contacts and interactions, or unexpected disturbances. The essence of our approach is schematically described in the figure below for a biped robot on a horizontal ground.
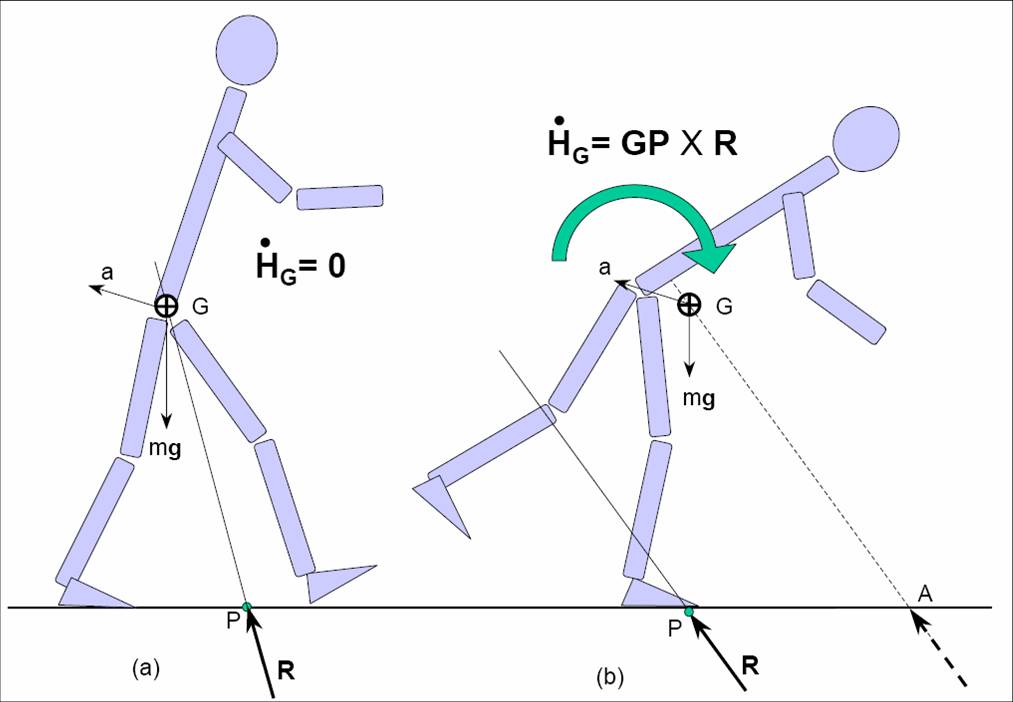
If the line of action of the GRF in Fig. b is linearly shifted, a time will come when the GRF will actually pass through the CoM. The point A on the ground through which this imaginary GRF now passes is called the centroidal moment pivot (CMP) point. The distance AP is a measure of rotational instability of the robot. Human beings do not have a direct control over GRF but must modulate it through dynamic coupling. This coupling is performed rather judiciously to take advantage of gravity. In normal walking, depending on the part of the gait cycle, the GRF may or may not pass through the CoM. There are interesting human movement examples, such as the take-off phase of forward running somersault, in which GRF is deliberately shifted to an off-centroid direction. This is useful in creating a large rotational instability which is what is precisely required for the task. Note that AP, the distance between CMP and CoP, is a measure of instability. It is meant to be primarily used as an analysis tool. It may be used as a control criteria with the following caveat. We, by no means, imply that to control CMP necessarily means to bring it to coincide with the CoP. In fact, a controller attempting to achieve this objective is likely to result in a rigid and restrictive gait. The fluidity of the human gait seems to come mostly from its cyclic regime of deliberate push to instability and a stability recapture. The following figure shows the relationships between a few ground reference points pertaining to the dynamics and balance of humanoid robots.
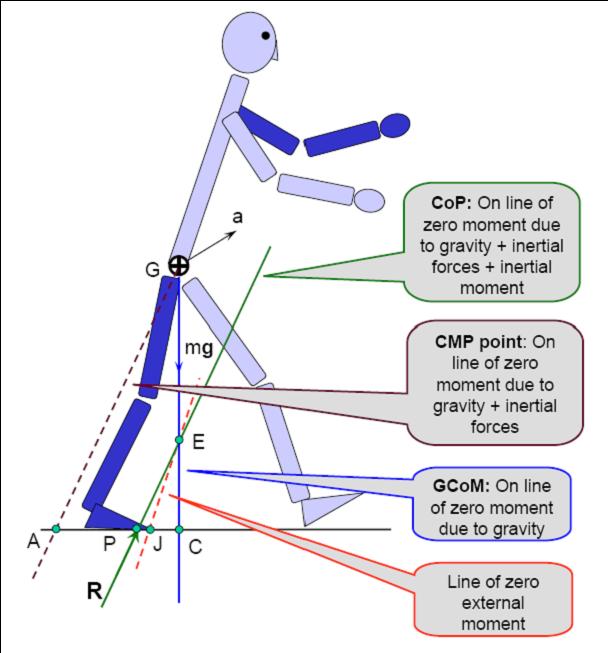
There is no difficulty in locating CMP for non-planar ground. Since CMP is the point of intersection of the GRF imagined to be passing through the robot CoM and the ground, the CMP definition is not inherently tied to a specific ground geometry.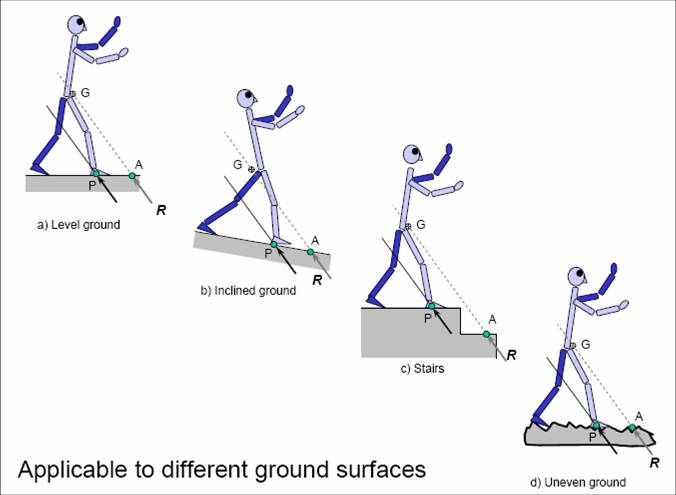 
Angular momentum also enhances push recovery ability of a humanoid.
|
A list of my papers on this topic:
-
M. B. Popovic, A. Goswami, and H. Herr,
Ground reference points in legged locomotion: Definitions, biological trajectories and control implications,
International Journal of Robotics Research, Vol. 24, No. 12, 2005.
(pdf).
Abstract: The zero moment point (ZMP), foot rotation indicator (FRI) and centroidal moment pivot (CMP) are important ground reference points used for motion identification and control in biomechanics and legged robotics. In this paper, we study these reference points for normal human walking, and discuss their applicability in legged machine control. Since the FRI was proposed as an indicator of foot rotation, we hypothesize that the FRI will closely track the ZMP in early single support when the foot remains flat on the ground, but will then significantly diverge from the ZMP in late single support as the foot rolls during heel-off. Additionally, since spin angular momentum has been shown to remain small throughout the walking cycle, we hypothesize that the CMP will never leave the ground support base throughout the entire gait cycle, closely tracking the ZMP. We test these hypotheses using a morphologically realistic human model and kinetic and kinematic gait data measured from ten human subjects walking at self-selected speeds. We find that the mean separation distance between the FRI and ZMP during heel-off is within the accuracy of their measurement (0.1% of foot length). Thus, the FRI point is determined not to be an adequate measure of foot rotational acceleration and a modified FRI point is proposed. Finally, we find that the CMP never leaves the ground support base, and the mean separation distance between the CMP and ZMP is small (14% of foot length), highlighting how closely the human body regulates spin angular momentum in level ground walking. -
S-H. Lee and A. Goswami,
Reaction Mass Pendulum (RMP): An explicit model for centroidal angular momentum of humanoid robots,
IEEE Int. Conf. on Robotics and Automation, Rome, Italy, April 2007.
(pdf).
Abstract: A number of conceptually simple but behavior rich “inverted pendulum” humanoid models have greatly enhanced the understanding and analytical insight of humanoid dynamics. However, these models do not incorporate the robot’s angular momentum properties, a critical component of its dynamics. We introduce the Reaction Mass Pendulum (RMP) model, a 3D generalization of the better-known reaction wheel pendulum. The RMP model augments the existing models by compactly capturing the robot’s centroidal momenta through its composite rigid body (CRB) inertia. This model provides additional analytical insights into legged robot dynamics, especially for motions involving dominant rotation, and leads to a simpler class of control laws. In this paper we show how a humanoid robot of general geometry and dynamics can be mapped into its equivalent RMP model. A movement is subsequently mapped to the time evolution of the RMP. We also show how an “inertia shaping” control law can be designed based on the RMP.
Kangkang Yin contributed an important correction to the above paper. (Correction)
Download animations:
HOAP2 Sumo motion with simultaneous RMP
Fujitsu HOAP2 gait with simultaneous RMP -
J. Pratt, J. Carff,
S. Drakunov and A. Goswami,
Capture Point: A Step toward Humanoid Push Recovery,
Humanoids2006, Genoa, Italy, December 2006.
(pdf).
Abstract: It is known that for a large magnitude push a human or a humanoid robot must take a step to avoid a fall. Despite some scattered results, a principled approach towards “When and where to take a step” has not yet emerged. Towards this goal, we present methods for computing Capture Points and the Capture Region, the region on the ground where a humanoid must step to in order to come to a complete stop. The intersection between the Capture Region and the Base of Support determines which strategy the robot should adopt to successfully stop in a given situation.
Computing the Capture Region for a humanoid, in general, is very difficult. However, with simple models of walking, computation of the Capture Region is simplified. We extend the wellknown Linear Inverted Pendulum Model to include a flywheel body and show how to compute exact solutions of the Capture Region for this model. Adding rotational inertia enables the humanoid to control its centroidal angular momentum, much like the way human beings do, significantly enlarging the Capture Region.
We present simulations of a simple planar biped that can recover balance after a push by stepping to the Capture Region and using internal angular momentum. Ongoing work involves applying the solution from the simple model as an approximate solution to more complex simulations of bipedal walking, including a 3D biped with distributed mass.
Download animations:
Push recovery with lunge only
Push recovery under increasing forward pushes
Push recovery under forward and lateral pushes -
M. Abdallah and A. Goswami,
A biomechanically motivated two-phase strategy for biped upright balance control,
IEEE Int. Conf. on Robotics and Automation, Barcelona, Spain, April 2005.
(pdf).
Abstract: Balance maintenance and upright posture recovery under unexpected environmental forces are key requirements for safe and successful co-existence of humanoid robots in normal human environments. In this paper we present a two-phase control strategy for robust balance maintenance under a force disturbance. The first phase, called the reflex phase, is designed to withstand the immediate effect of the force. The second phase is the recovery phase where the system is steered back to a statically stable “home” posture. The reflex control law employs angular momentum and is characterized by its counter-intuitive quality of “yielding” to the disturbance. The recovery control employs a general scheme of seeking to maximize the potential energy and is robust to local ground surface feature. Biomechanics literature indicates a similar strategy in play during human balance maintenance.
Download animations:
Recovery under potential energy control
Reflex and recovery against a 300N horizontal force
Robot balancing on a swaying table -
A. Goswami and V. Kallem,
Rate of change of angular momentum and balance maintenance of biped robots,
IEEE Int. Conf. on Robotics and Automation, New Orleans, April 2004.
(pdf).
In order to engage in useful activities upright legged creatures must be able to maintain balance. Despite recent advances, the understanding, prediction and control of biped balance in realistic dynamical situations remain an unsolved problem and the subject of much research in robotics and biomechanics. Here we study the fundamental mechanics of rotational stability of multi-body systems with the goal to identify a general stability criterion. Our research focuses on the rate of change of centroidal angular momentum of a robot as the physical quantity containing its stability information. We propose three control strategies using angular momentum that can be used for stability recapture of biped robots. For free walk on horizontal ground, a derived criterion refers to a point on the foot/ground surface of a robot where the total ground reaction force would have to act such that the rate of change of angulr momentum is zero. This new criterion generalizes earlier concepts such as GCoM, CoP, ZMP, and FRI point, and extends their applicability.
Back to main page |
Page last updated 2008